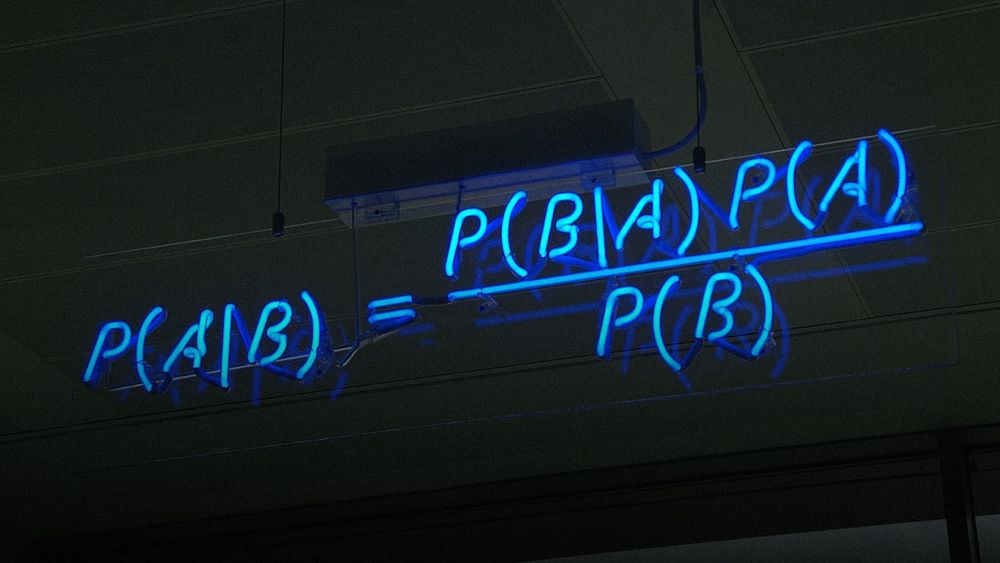P(A)=P(A∩B)+P(A∩Bc)
P = Probability
A = Any Event
Bc = Event
Literally everything we do is driven by this formula. It’s the flash calculation your brain considers with every breath you take and every move you make (did we just quote The Police?). It’s the formula that drives every decision in every aspect of our lives… even if we never stop to consider how it works.
Probability helps us define risk and measure reward. It helps us decide between forks in the road and it determines success, luck and failure. Probability is also how many traders make decisions…
And it’s why so few of them ever make any money.
There are 4 perspectives on probability:
Classical, Empirical, Subjective and Axiomatic. We’re going to focus on Classical.
Classical Probability allows us to define an expected value based on the odds of success. For example:
If the PowerBall lottery pool is currently worth $100M and the cost of a ticket is $1, then:
Expected value (lottery ticket) = prob(winning) X jackpot + prob(losing) X ($0) = (1 / 292,201,338) X ($100,000,000) + (292,201,337 / 292,201,338) X ($0) = $0.3422297. The ticket you paid $1 for is now worth $0.3422297 in your hand.
But if the lottery pool is $350M, then: = (1 / 292,201,338) X ($350,000,000) + (292,201,337 / 292,201,338) X ($0) = $1.197804. Now the ticket you paid $1 for is worth $1.197804 in your hand. But your odds of success haven’t changed (still 1 in nearly 300 million)
And then there’s taxes. Guh.
What does this have to do with probability in trading?
Well… nothing really… except far too many traders approach probability in trading as if it does.
Back in 2013, we conducted a study to try and determine the odds of success of each fractalerts pattern before it began, thereby adjusting our size and risk accordingly. We used Bayes Theorem which we briefly brought up in our blog about using trading robots. (Spoiler alert: Don’t… Just don’t).
In English, we wanted to consider the probability of the next trade being profitable if four of the last five were profitable, for example.
We used a range of 26 trades (half a year for us) and we took every variable possibility within that range (3 out of 7, 4 out of 19, 21 out of 26, etc). The range gave us 351 possibilities. We then tested two ways.
1: The odds of success on every single individual variable for every trade. We made a decision to buy or sell the next trade based on the success of the previous three trades. Then we tested the previous four trades. Then the previous five. This resulted in 26 different results.
2: The odds of success of the collective average for every variable. Every trade was based on the total probability of the 351 variable range.
(We also tested leveraged adjustments based on the odds of success… but that gets much more complicated and can be addressed another time).
We found our accuracy increased from roughly 60% to over 75%. At first glance, this looked like a 15% increase (75%-60% = 15%). At second glance, it could be described as a 25% increase (15%/60% = 25%). But in reality, this was a 100% increase of the odds in our favor (60/40 = 1.5 while 75/25 = 3). The golden ticket had been found.
Except… win rate has absolutely nothing to do with results… and neither does probability.
With these new found statistics, we went back in to our historical trades and adjusted exposure and risk according to the odds of success (exactly as we had tested). Accuracy truly did increase from 60% to 75%. But… and this is a big BUT… performance dropped by 30%.
By eliminating trades we otherwise would have taken (systematically and unemotionally), this test missed the most profitable trades simply because they did not fit within the expected probability. This test also enhanced many of the larger losses by over exposing on trades that were “probabilistically supposed to show a profit.”
Over exposure on losing trades and underexposing on winning ones. That never works out well.
How is that possible?
Classical probability increased the value of the lottery ticket and had no impact on the odds of success. Bayesian inference increased our odds of success and had no positive impact on our trading results (value).
Within trading, the frequency with which you are right or wrong has no impact on the next trade. You could have profited on 9 of your last 9 trades… but if that next one wipes out all of the profits from those previous 9, then no investor is going to listen to you say “yes, I lost money but I was right 9 out of 10 times.”
Probability, win rate, accuracy and other related words are often used by traders to determine success. These statistics are used to judge a revision to the mean and assume “well.. I’ve lost on my last three trades but my win rate is 60%, so my next trade should be a huge win.” These statistics are misleading and extremely dangerous for your account and should be avoided at all costs. Anyone advertising a probability of success has simply never actually placed a trade.
Trading is meant to be systematic and unemotional. Find out how fractalerts can simplify your trading at our Get Started page.
Services
